Aerospace Computational Engineering Lab
Research
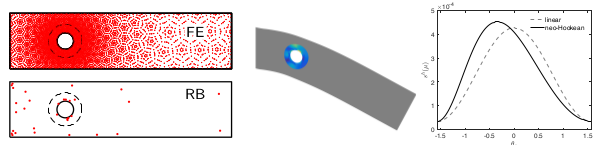
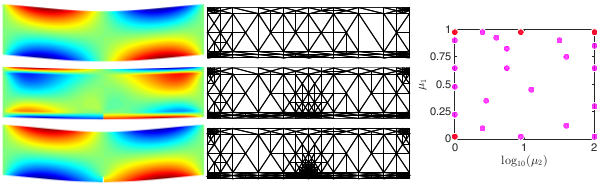
Model reduction for parametrized PDEs
The goal model reduction is to provide rapid and reliable solution of parametrized partial differential equations (PDEs). Model reduction is important in two scenarios: many-query scenarios in design, uncertainty quantification, inference, etc where the PDEs must be solved for a large number of different configurations; real-time scenarios in state estimation, control, etc where the PDEs must be solved in order of seconds. Our model reduction approaches are based on the idea of offline-online computational decomposition: in the offline stage, we construct, once, a reduced model through a relatively expensive training over the parameter domain; in the online stage, we invoke, many times, the reduced model.
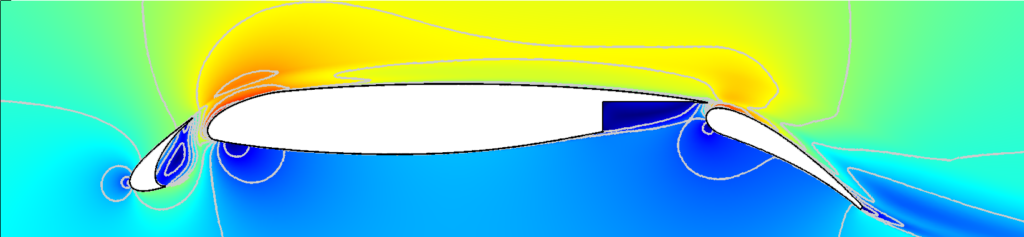
Adaptive high-order methods
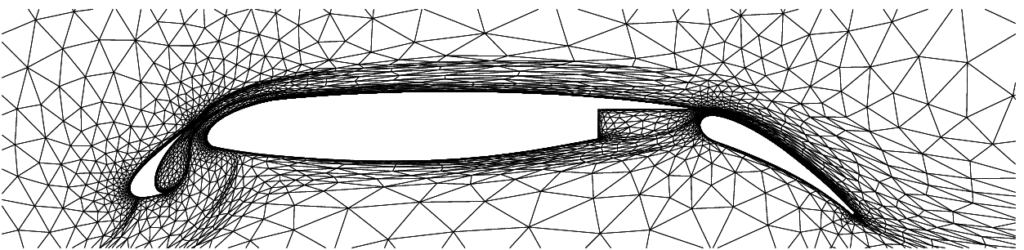
The goal of adaptive high-fidelity methods is to provide a reliable prediction of engineering outputs, such as lift and drag on an aerodynamic body, in an automated manner. The adaptive strategy that we work on builds on a discontinous Galerkin (DG) method, dual-weighted residual (DWR) a posteriori error estimate, and anisotropic hp mesh adaptation.
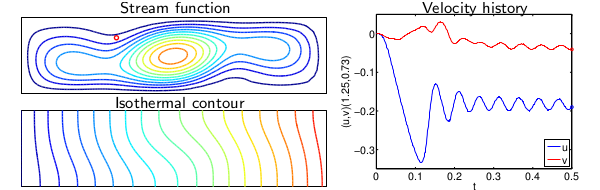
Data assimilation for engineering systems
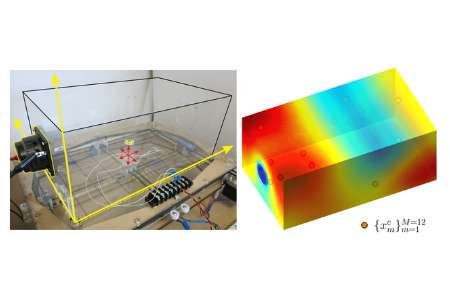
The goal of this project is to integrate mathematical models and experimental observations to assess and control both the discretization error and modeling error. The real-time assessment and control of the modeling error is particularly important for engineering systems that operate in the presence of uncertainties.